标签： 中位切分

中位切分法颜色量化

首先举两个例子。

有一种视频接口叫VGA，这种视频接口有一个最大的缺点，就是同一时刻无法显示超过256种颜色。而对于一张true-color的图片，R、G、B都是有1个byte标示，因此一张true-color的图片可能有2^24种颜色。这远远超过了VGA可以同时展示的颜色数量。

我们都知道有一种图片格式叫PNG(
PNG格式分析与压缩原理)。它的编码方案中，有一种使用调色板的编码方案。调色板上最多有256种颜色。这样每一种颜色都可以用一个byte的索引值代替。如果将一副超过256种颜色的png图使用调色板的编码方式，那么就可以明显的减少图片的体积。

那么如何将2^24种颜色用256种颜色表示呢？或者说，如何将m种颜色使用n种颜色来代替表示(m>n)。这就是这篇文章主要讨论的问题。

首先，如下图所示，RGB可以映射到三维空间中，R代表X轴，G代表Y轴，B代表Z轴。这样，任意一个RGB的组合都可以在空间中以一个点表示。

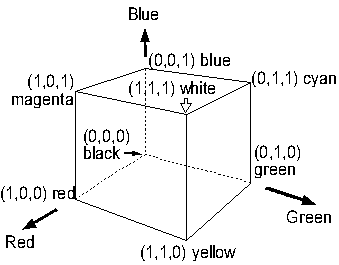
rgb-cube

对于一个24-bit的图片来说，通常来说颜色空间是连续的，因为颜色之间的最小差异是几乎不可能察觉的。现在，这个连续的颜色空间要被映射到256种离散的颜色上。将一个连续的变量映射到离散的集合上，就叫做量化。

有了上面这些说明后，现在有一张颜色很多的图片。图片上所有的点都被映射到一个空间中的立方体上。因为图片上点的分布一般不是均匀的，那么就可能有很多个点的聚集块。一般来说，聚集的越密，代表这些点的颜色越接近，那么如果我们将这些聚集块的点用聚集块中心点的颜色来表示，这样就可以将很多接近的颜色用一种颜色来代替。其实，这个过程跟聚类是很相似的。只不过一般的聚类算法都是无监督的机器学习，效率要较差。而中位切分法则可以用很快的速度完成这样的聚类。

中位切分法

中位切分法用简短的话描述：将一个图片对应的RGB立方体切割成目标数量的紧凑的RGB立方体，然后用立方体的质心值代表立方体内所有点的值。重复这个过程直到得到想要的颜色数量。

这里假设我们要获取256个颜色。详细的流程如下：

  • 将整张图片转换成一个RGB立方体
  • 找到立方体的最长边，从中位数的地方开始切割。得到两个包含相同数量点的立方体。
  • 对分割成的立方体重复上一步的切割过程直到得到256个立方体。
  • 256个立方体的质心就是要计算的256个颜色值。

用一个例子来说明（为了简单，这里没有B颜色空间）,这里有6种颜色，共14个点。想要得到4中颜色输出。

  1. 初始情况
Color (r,g)-coordinates Count
C0 (20,40) 3
C1 (40,20) 2
C2 (5,60) 4
C3 (50,80) 2
C4 (60,30) 1
C5 (80,50) 2
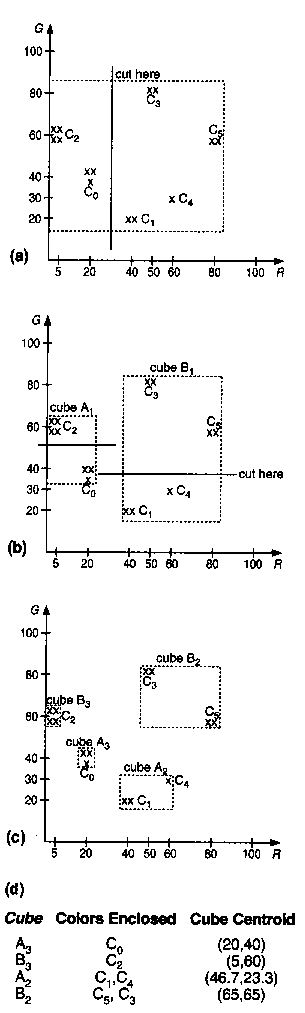
  1. 3次切割后的情况
Cube HistPtr.lower HistPtr.upper Colors Enclosed Cube Centroid
A3 0 0 C0 (20,40)
B3 1 1 C2 (5,60)
A2 2 3 C1,C4 (46.7,23.3)
B2 4 5 C5,C3 (65,65)

具体流程图如下：

第一次：最长边是Ｒ,中位数是（20 + 40) / 2 = 30。从30处切割。得到收缩后的矩形。左边的矩形为A1,右边为B1。
第二次: 切割B1的R边，得到A2,B2
第三次: 切割A1的R边，得到A3,B3

这个时候我们已经有4个矩形了。

这里我们有两个颜色映射方式。第一种是快速映射，以矩形的质心作为映射后的颜色值。第二种是最佳映射，得到和其他点的距离和最短的点作为映射后的颜色值。

切割过程

中位切分法的实现

  1. 递归方式。在描述的时候，我们RGB块描述成递归的方式。如下
Split(Cube){
  if (ncubes == 4) return;
  find longest axis of Cube;
  cut Cube at median to form CubeA, CubeB;
  Split(CubeA);
  Split(CubeB);
}

但是这种递归切割的方式是有问题的。结果如下图
递归切割

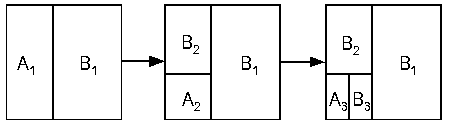
在递归情况下，B1将一直不会被处理。

2.为了解决1中的问题。我们可以设定一个最大深度(level)。比如我们要得到4个输出颜色。那么log 2 4=2。最大深度应该是2。当切割到最大深度时，我们就不再往下切割，转而切割那些还未被处理的更大的区域。

maxlevel = 2;
Split(Cube,level){
  if (ncubes == 4) return;
  if (Cube's level == maxlevel) return;
  find longest axis of Cube;
  cut Cube at median to form CubeA, CubeB;
  Split(CubeA, level+1);
  Split(CubeB, level+1);
}
  1. 但是这样又会有新的问题出现。如果一个立方体中只有一种颜色（实际上此时只有一个点)，不能再往下切割。因此我们需要一种方案去解决这个问题。这里可以维持一个包含所有立方体的数组，然后根据优先级排序切割。优先级可以按照level从小到大排序，但是所有颜色数量为1的立方体都会被忽略。这样每次切割前对这个数组做一次排序，取出优先级最高的立方体进行切割。直到切割出指定数量的立方体或者所有的立方体颜色都为1。
build initial cube from histogram;
set initial cube's level to 0;
insert initial cube in list of cubes;
ncubes = 1;
while (ncubes < maxcubes){
  search for Cube with smallest level;
  find the longest axis of Cube;
  find the median along this axis;
  cut Cube at median to form CubeA, CubeB;
  set CubeA's level = Cube's level + 1;
  set CubeB's level = Cube's level + 1;
  insert CubeA in Cube's slot;
  add CubeB to end of list of cubes;
  ncubes = ncubes + 1;
}

实践

  1. 使用中位切分法提取图片的主题色

  2. 使用中位切分法压缩图片

中位切分法的实现的go语言版本:joyme123/MedianCut。点击这里进行效果预览

参考文献

Median-Cut Color Quantization

前端图片主题色提取