树的可视化以及家谱绘制的算法

Contents

一、前言
二、难点
三、算法介绍

一、前言

树的可视化意思就是将一颗树（数据结构的树）用图形展现出来。树的可视化有很多种用途，比如说很常见的组织结构图就是树的可视化的应用。家谱也可以算是一颗树，但是与树的可视化稍微不同的是，会有配偶这个角色，同时一个家谱可能并不是从一个根节点向下（可能存在某个家族向上追溯到某一代，之前的资料已经完全丢失了，那么这个家谱的起源应该是这一代人，而不是具体到某一个人）。

二、难点

在树的可视化过程中，难点就在于如何确定每一个节点的位置（X,Y），Y坐标相对来说是比较好确定的，可以根据它在一颗树中的第几层来确定Y的值；X的值既受到同一层其他的节点位置的影响，同时也受到其子代位置的影响。因为其子代可能会和其兄弟节点的子代交叉。所以这篇文章主要讲解的是每个点的位置的计算。

家谱的绘制和树的可视化也有前言中的一些不同之处，因为也不能完全的将树的可视化算法生搬硬套。

下面我将一步步的讲解整个树的可视化算法的过程，以及如何将这个算法应用到家谱的绘制上，并给出具体的实现代码（因为是网页上有这个需求，所以代码是js写的）。算法的主要提出者是John Q. Walker II，这里有他对这个算法的相关讲解。POSITIONING NODES FOR GENERAL TREES

三、算法介绍

图1：
示意图

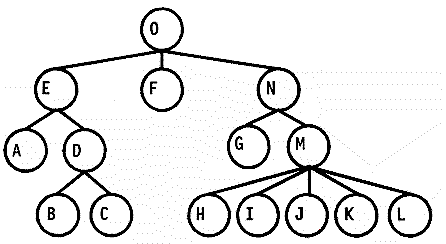
1、节点属性定义

var Node = function(key,image,description){
    this.key = key;
    this.parent = null;         //父辈
    this.offspring = null;      //指向最左边的子辈
    this.leftSibling = null;    //左兄弟
    this.rightSibling = null;   //右兄弟
    this.prelim = 0;            //x坐标的预定义
    this.modifier = 0;          //调整的大小
    this.level = 0;
    this.width = 60;            //每个节点的最终宽度，如果存在配偶这个宽度是会发生改变的
    this.height = 80;           
    this.nodeWidth = 60;        //每个节点的基本宽度，不会变
    this.nodeHeight = 80;
    this.x = 0;
    this.y = 0;
    this.spouses = [];
    this.image = image||"assets/post-photo.jpg";
    this.description = description || "";
};

这里首先介绍几个重要的属性：

parent,offspring,leftSibling,rightSibling：分别是当前节点的父节点指针、最左边的孩子节点的指针、左兄弟、右兄弟。以上图为例，M点的parent是N,offspring是H,leftSibling是G,rightSibling是null。

prelim：当前点的X的预定义位置。如同在难点中所说，X的位置受到很多因素的影响，所以需要多次计算。prelim只是预定义的位置，不是最终的位置。

modifier：调整值，不过这个调整值并不是说当前点的X还要调整多少，而是当前点的后代的X还要调整的大小。

level：当前点所处的层级。

width、height、nodeWidth、nodeHeight：这些参数用来表示节点的宽和高，width和nodeWidth的区别在于，nodeWidth是画出来的节点的宽度，是一个基本属性，不会改变，width则表示这个点最终会占用的宽度。在树的可视化算法中，只需要nodeWidth和nodeHeight，width和height是专门为家谱的绘制增加的。

x：当前点的X，如何确定X的大小呢？以M为例，M.X = M.prelim + N.modifier + O.modifier。

y：当前点的y,以M为例: M.y = M.level * (每层的间隔 + M.height);

spouses:这个是专门为家谱的绘制准备的。表示当前点的配偶，一个点的配偶可以有多个，所以使用数组。

2、算法的大概流程

算法大概可以划分为：

1.倒序遍历整颗树，初次确定每个点的prelim和modifier。
2.从最底层逐级向上检查是否存在交叉，如果存在交叉则调整（这一步和我参考的算法不同，它是从上向下检查，但是我在使用中发现，如果存在子树的子树交叉的情况，那么在高层做了调整之后，这里再做一次调整就可能出现再次重叠的情况，所以改用从底层向上检查）。
(勘误：这个地方不对，应该还是从上向下遍历，这样从上方调整后，即使下方还有重叠，也可以再次检测并调整)
3.最后确定根节点的位置

3、算法详细介绍

这里我们先定义几个常量:

SiblingSeparation = 4,   //兄弟节点之间的间隔
SubtreeSeparation = 6,   //子树之间的间隔
width = nodeWidth = 2   //节点的宽度

还是以图1所示的树为例，这里先做一遍倒序遍历，初步确定每一个节点的位置：

A：因为A的左节点是null,所以

A.prelim = 0;
A.modifier = 0;

B.prelim = 0;
B.modifier = 0;

C：因为C有左节点B，所以C要在B的基础上做向右的偏移，偏移量为B的prelim加上B的宽度加上间隔大小(这个地方的处理和John Q. Walker II的算法不同，是为了家谱的显示做的更改)。所以

C.prelim = B.prelim + B.width + SiblingSeparation = 0 + 2 + 4 = 6;
C.modifier = 0;

D：因为D是B、C的父节点，同时是A的右兄弟，所以D的位置由A确定后，为了保证D应该在B和C中间，应该对B、C做调整，但是我们并不会再回头对B、C做处理，而是计算D的modifier，以此来表示D的后代需要调整的位置。并且D.modifer应该等于D.prelim – (B.prelim + C.prelim)/2。

D.prelim = A.prelim + A.width +  SiblingSeparation= 0 + 2 + 4 = 6;
D.modifier = D.prelim - (B.prelim + C.prelim) / 2 = 6 - (0 + 6) / 2 = 3;

E：因为E没有左兄弟，所以直接通过A、D来确定位置即可

E.prelim = (A.prelim + D.prelim) / 2 = (0 + 6) / 2  = 3;
E.modifier = 0;

F：

F.prelim = E.prelim + E.width + SiblingSeparation = 3 + 2 + 4 = 9;
F.modifier = 0;

G：

G.prelim = 0;
G.modifier = 0;

H：

H.prelim = 0;
H.modifier = 0;

I：

I.prelim = H.prelim + H.width + SiblingSeparation = 0 + 2 + 4 = 6;
I.modifier = 0;

J：

J.prelim = I.prelim + I.width + SiblingSeparation = 6 + 2 + 4 = 12;
J.modifier = 0;

K：

K.prelim = J.prelim + J.width + SiblingSeparation = 12 + 2 + 4 = 18;
K.modifier = 0;

L：

L.prelim = K.prelim + k.width + SiblingSeparation = 18 + 2 + 4 = 24;
L.modifier = 0;

M：

M.prelim = G.prelim + G.width + SiblingSeparation = 6;
M.modifer = M.prelim - (H.prelim + L.prelim) / 2 = -6；

N.prelim = F.prelim + F.width + SiblingSeparation = 9 + 2 + 4 = 15;
N.modifier = N.prelim - (G.prelim + M.prelim) / 2 =  12;

走到这里我们就不再向上走了，因为根节点的位置肯定是有E和N来最终确定。所以这个时候应该来调整整颗树，检查是否存在节点位置重叠的情况。检查是否重叠是一个递归，所以使用递归检查会降低很多复杂度。但是这里我们走一遍过程，并非是严格按照代码执行过程。

我们先检查最底层，也就是这颗树的第4层：
检查C和H是否有重叠（当然是最右和最左做对比了）：
C.X = D.modifier + E.modifier + C.prelim = 3 + 0 + 6 = 9;
H.X = M.modifier + N.modifier + H.prelim = -6 + 12 + 0 = 6;

所以H在C的左边3处，显然是重叠了的。所以需要将H所在的子树全部向右移offset = SubtreeSeparation - (H.X-C.X) = 9;我们一直向上找，直到C和H的祖先是兄弟时，也就是E和N，修改N.prelim、N.modifier就代表将N和其子树全体右移。

N.prelim = N.prelim + offset = 15 + 9 = 24;
N.modifier = N.modifier + offset = 12 + 9 = 21;

这时候E和N之间距离变得更大了，但是E和F的距离与F和N的距离是不同的，为了让树显示的好看一点

F.prelim = F.prelim + offset / 2 = 9 + 9 / 2 = 13.5;

F的子树也应该调整一下（虽然这里并没有）

F.modifier = F.modifier + offset / 2 = 0 + 9 / 2 = 4.5;

我们再往上看，发现已经没有重叠的了。

这时候确定根节点O的位置

O.prelim = (E.prelim + N.prelim) / 2 = (3 + 24) / 2 = 13.5;
O.modifier = 0;

四、如何将树的可视化算法应该到家谱的绘制上。

在之前已经介绍过家谱和树的结构有稍许不同，所以我们尽量将家谱做一些处理，使其变成标准的树结构。

1.配偶问题。
将某个节点的配偶不当成一个节点看待，而是这个节点的一部分，所以我们只需在有配偶的时候改变节点的width就可以了。
2.不只一个根节点的问题
既然有不只一个根节点存在，那么我们就自己定义一个虚拟的节点作为根节点，将第一层所有的点的parent都指向这个根节点即可。这样就是一个非常标准的树结构了。

五、源代码

源代码放在了github上，地址为https://github.com/joyme123/candraw